In this post we describe joint work with our collaborators at QSimulate to develop the Fermionic Quantum Emulator, a fast emulator of quantum circuits that simulates the behavior of electrons. Efficiency gains in this particular area are exciting because simulating fermions is known to be challenging and an area we suspect to have a substantial quantum advantage. The Fermionic Quantum Emulator (FQE) adds to our portfolio of simulators for quantum hardware, quantum error correction, and quantum circuits and provides the capability to simulate even large quantum systems in an effort to evaluate beyond classical physics simulations. The emulator slots into our set of open source software tools for quantum information and is completely interoperable with OpenFermion. The code is Python based with C-extensions for computational hotspots letting us gain performance without sacrificing readability or ease of distribution. For complete details, see the open access publication or check out the code!
Prelude: The cost of quantum simulation
To store the vector of numbers at double precision representing the wavefunction of 26 qubits requires approximately 1 Gigabyte memory. By the time we add 10 more qubits to our calculations we need a Terabyte of memory. In terms of simulations of molecules or materials, 36 qubits is quite small–translating to a modest accuracy simulation of the electrons in diatomic or small molecules. Simulations of electrons in more complicated molecules can require hundreds of qubits to accurately represent nature and provide the scientific insight chemists need to reason about reaction mechanisms. What this means for quantum algorithm developers who focus on physics simulation is that even testing algorithms at a small scale prior to running them on a quantum device can be a serious computational undertaking.We can temper the exponential scaling of direct simulation by exploiting physical symmetries when we know our circuits are simulating a particular type of quantum particle. If we allow ourselves to move away from direct simulation of the quantum device and relax our simulation requirements to emulation we get a lot more wiggle room in terms of algorithm design. The Fermionic Quantum Emulator takes this approach to circuit simulation and achieves substantial computational advantage over generic quantum circuit simulators that do not make physical symmetry considerations.
The Fermionic Quantum Emulator:
The Fermionic Quantum Emulator (FQE) is a state vector simulator that takes advantage of common symmetries of fermionic spin-1/2 systems which can drastically reduce the memory required to represent a quantum state in memory. Using a symmetry-reduced wavefunction representation allows us to make further algorithmic improvements when simulating arbitrary fermionic generators (many-body quantum gates) and standard non-relativistic chemical Hamiltonians. These improvements are obtained by adapting algorithms developed in the theoretical chemistry community for exact fermionic simulations.
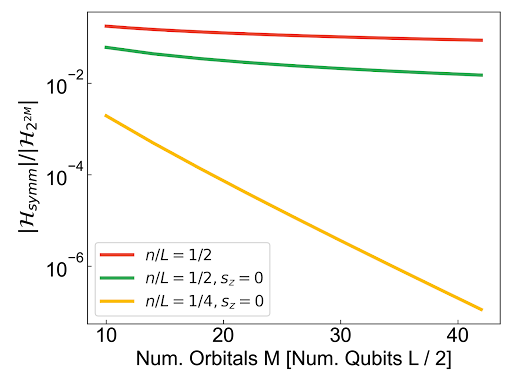
For a system where the number of electrons is equal to half the total qubits required to simulate the system we see modest improvements and can store a 36 qubit wavefunction with 37 Gigabytes of memory–substantial savings when considering the qubit wavefunction without symmetries considered requires 1000 Gigabytes. For lower filling systems we see even more substantial advantages. To emphasize this point we plot the ratio of the sizes required to represent wavefunctions in the symmetry-reduced representation used by FQE and the more expensive qubit representation.
Emulating quantum circuits pertaining to fermionic dynamics allows us to be more clever with our simulation algorithms instead of a direct simulation of the quantum gates. For example, instead of translating fermionic generators to qubit generators using standard techniques the FQE provides routines for directly evolving common circuit primitives and arbitrary fermionic generators. The structure of common algorithmic primitives, such as basis rotations or diagonal Coulomb operators, allows us to write very fast routines for evolving symmetry-reduced wavefunctions. Below we plot the performance of one of these primitives (basis rotations) and compare the performance of FQE with a highly optimized Qsim program written in C++. In both a single threaded and multithreaded regime the FQE outperforms Qsim by at least an order of magnitude; clearly demonstrating that physics and symmetry considerations coupled with algorithmic improvements can have substantial computational advantages.
The FQE is completely interoperable with OpenFermion but can also be used as a standalone fermionic simulator. We have built in functionality that generates many standard sets of observables for fermionic simulation (arbitrary expectation values and reduced density matrices). The FQE also has custom routines for standard quantum chemistry Hamiltonians that further exploit the symmetry in a spin-restricted setting for more computational efficiency.
The FQE is, and will remain, Apache 2 open source. We welcome pull requests, issues, or general commentary on how we can improve the emulator. Our hope is that you can use the FQE to accelerate explorations of quantum algorithms, as a general purpose tool for simulating time-dynamics of fermions, and as the start of a family of methods for emulating fermionic circuits. To get started check out this tutorial and this example on simulating spin-charge separation in the Fermi Hubbard model.
We depend on simulations to understand which problems quantum computers may be able to solve, and when. The FQE enables us to stretch further into the realm of difficult simulations of fermionic systems and increase our research velocity. Looking forward, the FQE is the start of a general framework for extending various qubit simulation techniques to the fermionic setting which will help us define the frontier of quantum computational relevancy and quantum simulation advances.
By Nicholas Rubin - Senior Research Scientist
For a system where the number of electrons is equal to half the total qubits required to simulate the system we see modest improvements and can store a 36 qubit wavefunction with 37 Gigabytes of memory–substantial savings when considering the qubit wavefunction without symmetries considered requires 1000 Gigabytes. For lower filling systems we see even more substantial advantages. To emphasize this point we plot the ratio of the sizes required to represent wavefunctions in the symmetry-reduced representation used by FQE and the more expensive qubit representation.
The ratio of memory requirements for circuit simulation when considering physical symmetries versus direct simulation of qubits. Chemistry and materials Hamiltonians commute with the number and spin operators so we can focus on simulating the wavefunction in only the relevant symmetry sectors. As shown by the yellow line (quarter filling) this can lead to substantial savings. For a quarter filling wavefunction on 48 qubits (24 orbitals) we would need 290 Gb and a qubit simulation would require 4.5 Petabytes.
CPU Walk clock time for the the basis rotation primitive C-kernel primitive versus an equivalent circuit evolution time with Qsim.
The code, getting involved, and future directions:
The FQE is a python package with easily extensible modules for maximum flexibility. We have accelerated some computational hotspots with C-kernels and provide users the ability to easily toggle between these two modes. The C-kernels are further accelerated with OpenMP. Installation uses the standard python C-extension workflow and does not require specific linking to BLAS routines. Pointers to these routines are obtained from Numpy and Scipy lowering burden programmers and computational physicists using the software.The FQE is completely interoperable with OpenFermion but can also be used as a standalone fermionic simulator. We have built in functionality that generates many standard sets of observables for fermionic simulation (arbitrary expectation values and reduced density matrices). The FQE also has custom routines for standard quantum chemistry Hamiltonians that further exploit the symmetry in a spin-restricted setting for more computational efficiency.
The FQE is, and will remain, Apache 2 open source. We welcome pull requests, issues, or general commentary on how we can improve the emulator. Our hope is that you can use the FQE to accelerate explorations of quantum algorithms, as a general purpose tool for simulating time-dynamics of fermions, and as the start of a family of methods for emulating fermionic circuits. To get started check out this tutorial and this example on simulating spin-charge separation in the Fermi Hubbard model.
We depend on simulations to understand which problems quantum computers may be able to solve, and when. The FQE enables us to stretch further into the realm of difficult simulations of fermionic systems and increase our research velocity. Looking forward, the FQE is the start of a general framework for extending various qubit simulation techniques to the fermionic setting which will help us define the frontier of quantum computational relevancy and quantum simulation advances.
By Nicholas Rubin - Senior Research Scientist